iRRAMx: a static C++ library for scientific computations
Introduction
iRRAMx is a static C++ library that provides functionalities for rigorous scientific computations based on iRRAM, a C++ library that provides exact real computation. It provides data type REAL for real numbers and primitive operators for the field arithmetic of real numbers. Numbers are computed exactly in the sense that they do not introduce any rounding errors! Going beyond and based on those primitive operations, this extension provides more advanced data types and operations for continuous mathematics.
This had been conducted by Complexity and Real Computation lab. My task was to make an abstract data structure for Compact subsets in Euclidean space, providing
- Membership checking, and
- Drawing figure(for 2D) in exact real computation.
Implementation
Based on iRRAM, all codes are written in C++.
Examples
| Image | Name | Formula |
|---|---|---|
 |
Unit square | \(f:[0,1]^2 \times \mathbb{N} \rightarrow \lbrace 0,1 \rbrace\) \(f(u,v,p)=1\) if the distance from \((x,y)\) to unit rectangle is less than \(2^{-p}\) |
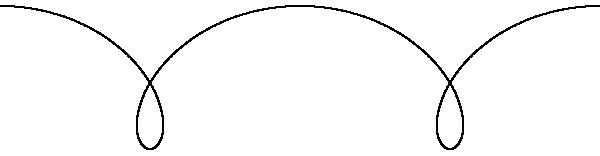 |
Prolate cycloid | \(f:[0,1] \rightarrow \mathbb{R}^2 \) \(f(t) = (16\pi t+3\sin(8\pi t), 3\cos(8\pi t)) \) |
 |
Whirl | \(f:[0,1] \rightarrow \mathbb{R}^2 \) \(f(t)=(8\pi t \cos(8\pi t), 8\pi t \sin(8\pi t))\) |
 |
Filled sin function | \(f:[0,1]^2 \rightarrow \mathbb{R}^2 \) \(f(u,v) = (6\pi u, v\sin(6\pi u))\) |
 |
Whirl 2 | \(f:[0,1]^2 \rightarrow \mathbb{R}^2 \) \(f(u,v) = (r\cos\theta, r\sin\theta)\) where \(r = 4 \pi u, \theta = 4 \pi u(2v+3)/5\) |